Elliptic Curve Cryptography Encryption- Elliptic curve cryptography encryption is a common current public key cryptographic technique that is more efficient, faster, and smaller than most other cryptographic systems. The elliptic curve theory underpins ECC, which allows for the development of more efficient cryptographic keys. ECC’s asymmetric encryption also has smaller key sizes, making it more lightweight.
Getting to Know ECC
Existing public encryption algorithms, such as RSA and Diffie-Hellman, produce enormous numbers that necessitate a lot of computing power. As a result, they require a lot of resources to encrypt apps, making them unsuitable for resource-constrained mobile apps. The usage of elliptic curves allows for the construction of more efficient and faster keys. The elliptic curve equation characteristics of ECC provide mathematically robust and sophisticated keys, resulting in a higher level of security. Furthermore, elliptical curve cryptography uses shorter key lengths to provide more secure security, making it ideal for securing mobile apps.
ECC’s applications
For prominent cryptocurrencies like bitcoin, ECC encryption is one of the most often utilised application methods for digital signatures. For cryptography and transaction signing, cryptocurrencies use the Elliptic Curve Digital Signature Algorithm (ECDSA) key. During key pair and key exchange, elliptic curve cryptography is used in digital signatures with an ECDSA key. Because of the cheap resources required, several parts of SSL standards use ECDSA signing SSL certificates. Other ECC applications include:
- Proving ownership of cryptocurrencies such as bitcoins is a difficult task.
- Keeping the US government’s internal communications and secret data secure
- Anonymity for users of the TOR project is maintained and preserved.
- In Apple’s iMessage messaging service, providing encryption signatures
- Secure web browsing is enabled.
Is ECC Different from Other Public Key Encryption Methods?
ECC cryptographic algorithms are used for the same reasons that RSA cryptographic algorithms are used. Both RSA and ECC, for example, generate a private key and a public key infrastructure to let two individuals or devices to securely communicate by exchanging a shared secret. ECC public key encryption algorithms, on the other hand, have some advantages over RSA and other encryption systems. A 256-bit ECC key, for example, gives about the same level of security as a 3072-bit RSA key. Furthermore, the elliptic curve encryption technique allows systems with limited resources, such as CPU power, to use around 10% of the bandwidth and storage space required by RSA algorithms.
Because ECC is based on elliptic curve theory, it generates encryption keys using the features of the elliptic curve equation. The method differs from the standard way of generating huge prime numbers, which uses public-key cryptography algorithms. Diffie-Hellman and RSA are two public-key cryptography algorithms that can be utilised with the ECC encryption technology. According to research, ECC cryptographic systems can encrypt and safeguard data using a 164-bit key, but other systems would need a 1,024-bit key to achieve the same level of security. ECC security techniques are favoured for protecting mobile applications because they use short keys to give good protection while using less battery and computer power.
ECC Trapdoor Function
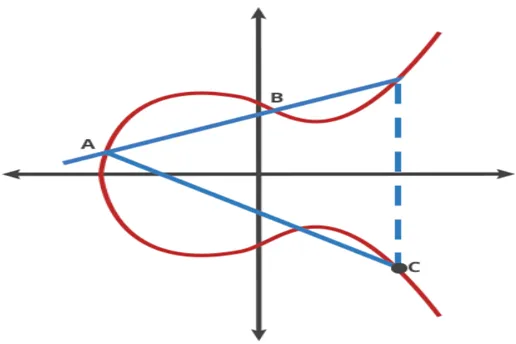
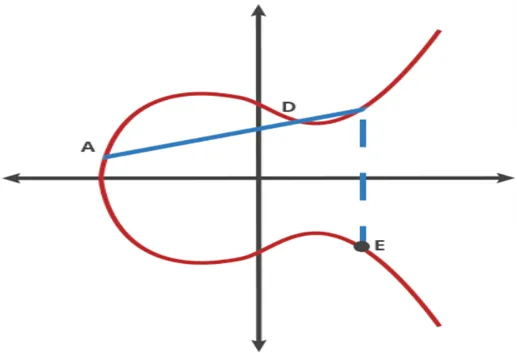
One of the fundamental reasons the elliptic curve key is more effective and different than the RSA cryptographic key is because of the ECC trapdoor function. The ECC encryption method uses the trapdoor function, which is a mathematical algorithm. The algorithm incorporates the number of hops required to reach certain sites and operates as follows:
- First, you start on an arbitrary point on an elliptic curve and use the dot function to locate a new point.
- When you start at A:
- A dot B =-C (connect points A and B with a line that intersects at -C).
Source Ars Technica
- Reflect from –C to C across the X-axis and A dot C = -D (connect A and C with a line that intersects at -D).
Source Ars Technica
- Reflect from –D to D across the X-axis and A dot D = -E (connect A and D with a line that intersects at -E).
Source Ars Technica
- Reflect from –E to E across the X-axis.
This is a nice trapdoor function because it is simple to discover the ending place (E) if the user knows the starting point (A) and the hops required to get there. However, determining the number of hops required is difficult if the user only knows the starting and ending points. ECC encryption uses the same principle, with the public key representing the beginning EC point A and the private key representing the number of hops required to travel from A to E.
The Benefits of Using ECC
In comparison to RSA and other public cryptography algorithms, ECC keys are smaller and more efficient. As a result, elliptic cryptography based on public-key encryption is quicker to process but more difficult to decrypt. RSA encryption, on the other hand, is based on the idea that a product of huge prime numbers multiplied is simple, but factoring the result back to the original prime numbers is difficult.
In this case, a 256-bit ECC key is comparable to a key length of 3072 bits. ECC cryptography benefits from the use of smaller, simpler, and more efficient ECC keys. It outperforms RSA cryptography algorithms in terms of resource and energy consumption in small mobile devices.
Furthermore, ECC encryption is frequently used in conjunction with Diffie-Hellman encryption to improve efficiency. ECC encryption doesn’t execute the communication and authentication duties of RSA, but it does generate the ephemeral DH session key with the help of an elliptic curve private key. ECDHE-RSA encryption is included in the linked SSL cypher suites, which complements DHE-based cypher suites.
The main advantage of utilising elliptic curve cryptography with Diffie-Hellman (ECDHE-RSA) over ordinary Diffie-Hellman (DHE-RSA) is that it has optimised efficiency and gives a same degree of protection with fewer keys.
While there are certain worries about adopting ECC certificates, which involve a source of random numbers for signatures, the advantages of elliptic curve encryption exceed the disadvantages of the standard RSA algorithm. Furthermore, new technologies such as quantum computing put standard public encryption methods at danger, making ECC encryption a feasible alternative choice.











FIND US ON SOCIALS